Well, we’ve got some football tonight. Let’s get some potentially upsetting news out of the way up front: Advanced Sports Analytics will not be providing pre-season projections, our thinking around this is two-fold:
Standard predictive models that can deployed for the regular season have next to no useful application for pre season games. The reasoning for this should be obvious, the factors that govern a regular season NFL game are vastly different from the factors that govern pre season games.
Our approach has always been data- & modeling-centric. We feel the value of this approach is vastly diminished in pre season.
Hopefully everyone reading understands our thinking on this, we feel that there is simply too much work to prepare for the NFL regular season to be derailed by pre season modeling & data work.
One of the workstreams we’ve been working on in preparation for the regular season is the creation of a player prop betting model & front end tool. The initial version of this tool can be found here:
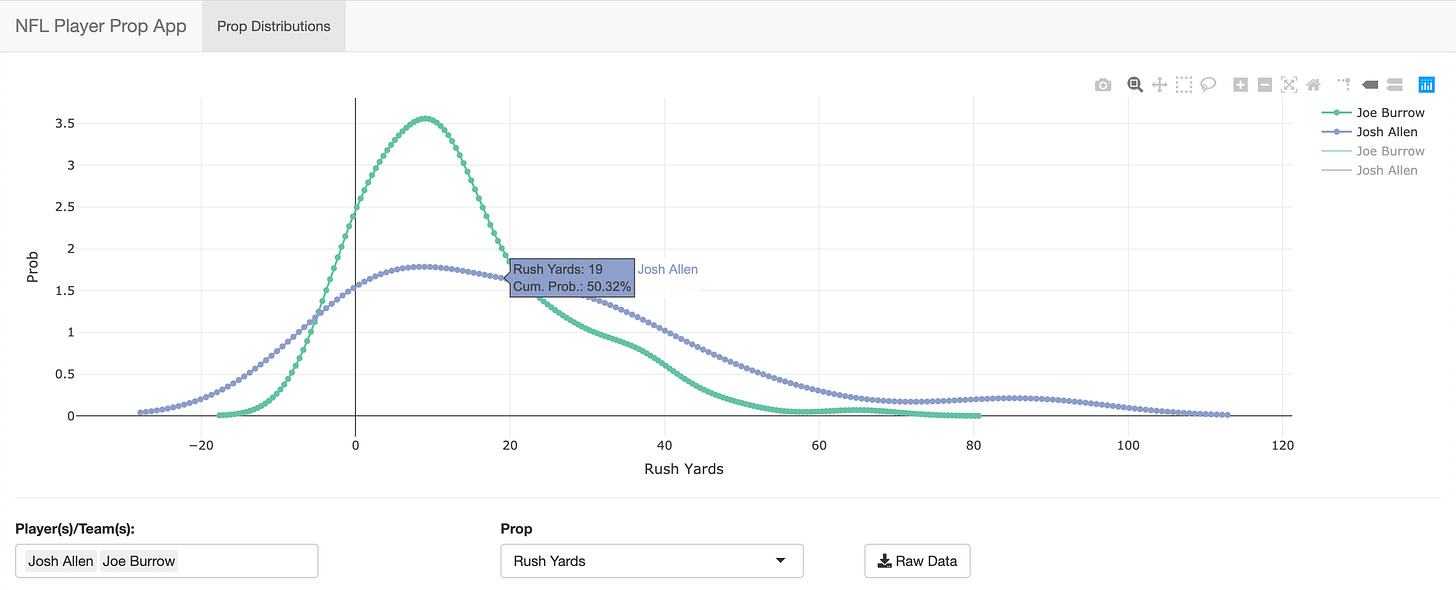
As of now, users can search players and their different probabilistic projections with regards to different statistical categories. Quarterbacks have passing & rushing yards & touchdown projections, running backs rushing & receiving, wide receivers & tight ends receiving yards & touchdowns and receptions.
Let’s first talk about how to interpret probabilistic projection before we dive into the nuts & bolts, and how it differs from traditional DFS projection. Before we dive in, please note that there is a lot of projection fine-tuning that must occur before Week 1 - line/total movement, projecting player rush & target shares, weather, et al. This is not meant to be a discussion of specific bets or probabilities, but rather a discussion of using probabilistic projection for prop bet consideration.
For prop bets, we’re likely betting on the binary outcome of whether or not a player achieves above or below a specified statistical total. Probability distributions, like the ones above, show an x-value (a statistical outcome) and the associated probability of that outcome occurring (y-value). For the purposes of prop betting, the “cumulative probability” of outcomes are of central importance. Cumulative probability can simply be understood as the probability that a statistic is less than or equal to a specific value. In the example above, our cursor hovers over an x-value of 19 yards, which for Josh Allen has a cumulative probability of 50%, making it the median outcome. Cumulative probability always is represented as the probability of less than or equal to, but we calculate the probability of greater than a value as simply 1 - cumulative probability. So if you hover over the x-value of 40 yards, you’ll see that Josh Allen has an 80% cumulative probability, meaning that there is an 80% chance he rushes for less than or equal to 40 yards, 20% chance he rushes for more.
As you can see, this is exceptionally useful for prop betting. Based on the above distribution, if we were presented with a prop bet Josh Allen over/under 19.5 rushing yards, -105 odds, we could quickly calculate the expected value of both sides of this bet. Note that expected value is the sum of outcome values times probability of said outcome.
Bet over: 50% * 1.95 units (50% chance of > 19.5 yards, 1 + 105/100 is the number of units won per winning bet), equals 0.975 units won per unit bet, negative expected value bet.
Bet under: 50% * 1.95 units, -0.025 EV per unit bet.
Per our projection, a 19.5 Allen rushing over/under is an efficient and, at -105, a -EV bet on either side. However, if we were presented with say a 26.5 rushing over/under for Allen (at -105), the +EV side should be clear (as per probability distribution).
Bet under: 61.5% * 1.95 units, +0.2 EV per unit bet.
This approach can even be useful for bets with uneven odds. If we were presented with a bet of Allen 2.5 pass TDs with -170 under & +160 over odds, we could take to cumulative probability to evaluate.
We can see that the cumulative probability for 2 or fewer Allen passing touchdowns is 60%, meaning that the probability he goes over 2.5 (3+ pass TDs) is 40%.
Bet over: 40% * 2.6 units = +0.04 EV per unit
Even though we think it is more likely than not that Allen goes for fewer than 2.5 TDs, the hypothetical odds are favorable enough for the over that betting over 2.5 is positive expected value.
I want to close with a discussion about how this approach differs from traditional DFS projection, and why this probabilistic approach offers more utility than our traditional DFS projections - although as you likely know, considering DFS outcomes probabilistically is an important nuance.
For predicting DFS outcomes, our position is that attempting to project player means is far more more important than trying to predict player medians. Take the extreme example (as a thought exercise) of a running back that has two possible outcomes with regards to receptions: 75% chance of getting zero receptions, 25% chance of getting 10 receptions. For DFS purposes, this running back would be a phenomenal play - while there is a 75% chance he is a total dud, there is a 25% chance that he is an absolute slate-breaker. His mean reception projection is 2.5 catches, his median projection is 0 catches. A system that incorporates players’ outcome range & probabilities of course is good for this purpose. In DFS, outcomes are not binary success/failures, the degree to which a player succeeds/fails is significant. However, for prop betting purposes, the degree of success/failure is negligible. A mean-based projection system, which would suggest a mean outcome of 2.5 catches would suggest betting over on a 1.5 catch prop, which would be a losing bet in the long run.
While the above example isn’t really plausible, we do still get get non-symmetrical distributions in the real world. Take Dalvin Cook for example - who in 2020 averaged more than 3 receptions per game, but had 2 or fewer catches in 8 of 14 games (57%).
If we were to approach projecting Cook’s catch total using some sort of regression model - which aims to reduce error, tends to be more of a mean-oriented model - we might come to the conclusion that betting over 2.5 receptions at even money is a slam dunk bet. However if we look at possible outcomes probabilistically, we might be inclined to lean towards the under.
For DFS purposes, we are content to use regression-based projection approaches. While simple linear regression (which assumes a normally distributed response variable, which isn’t always true for DFS) can give us singular predictions and also a range of outcomes & their probabilities (using calculations like standard error), most complex regression algorithms will give us “point predictions”. A point prediction is, as the name suggests, a prediction of a single point, no context as to the likelihood of alternative outcomes near that point. This can be fine for DFS purposes, as fantasy points are truly continuous outcomes. But for prop bets on statistics like touchdowns & receptions - which are measured in numeric integers, but tend to behave more as discrete outcomes - point projections can sometimes be less valuable. If we project a player to rush for 0.8 touchdowns (using a regression model), what does that actually mean? A player can’t score a fraction of a touchdown - does that mean said player has an 80% chance of scoring a touchdown? Does that mean the player is more likely than not to score a touchdown or more? In 2020, Cam Newton averaged 0.8 rushing touchdowns per game, but scored a rushing touchdown in only 8 of 15 games. When dealing with discrete (or vaguely-discrete outcomes like receptions), point predictions of 2.5 don’t necessarily mean equal probabilities of realized outcomes of 2 & 3. As such, for prop betting we prefer an approach that does allow us to model out a range of possible outcomes and their associated probabilities, whether symmetrical or asymmetrical.
As of now, the approach we’ve landed on is called “K-nearest neighbors”. In short, this approach considers a player’s underlying variables (like any model), and looks to past outcomes of players who have similar underlying variables, their “neighbors”. Not all neighbors are equally similar, as such we calculate neighbors’ “distance” from the projection player, and use the inverse of that distance as a proxy for the probability of the projection player replicating the neighbor’s outcome. That is, the closer (lower distance measure) a neighbor is, the higher probability of the projection player repeating their outcome. Then, with a list of neighbors and their realized outcomes & probabilities, we sample (you’ve probably heard sampling from a probability set or distribution referred to as “simulating”).
As we continue to build out our tools for the 2021 NFL season, I want to continue ASA’s development of point prediction models. For DFS purposes this remains a really good catch-all model type for mean projections. But I also want to work to build out our projections with consideration for asymmetrical outcome probabilities, as this will be crucial for building good prop betting tools as well as DFS tools & models.