Getting Ready for NFL: Simulations
Pre Season | Week 2
We have a sneaking suspicion that a popular talking point for the 2021-22 NFL season will be “sims” - and rightfully so. The skilled DFS tournament player likely understands that the goal of tournament lineup construction is not to optimize towards expected fantasy points, but rather expected contest return given certain assumptions. Optimizing towards fantasy points is, for hopefully obvious reasons, a far simpler task - one must take a set of projections and find the combination (or have a computer find the combination) that maximized projected fantasy points under known contest constraints.
However, for tournament purposes, optimizing towards lineup expected value is a far more complex task. Off the cuff, there are three primary variables that we must account for when building lineups.
Ownership - The rate at which a player is owned should impact our interest in playing them. In a vacuum, a QB that we estimate as 50% probability of being the best value at his position should be a player we seek to roster. But if 90% of the field rosters that QB, the relative value of not rostering him will actually increase significantly.
Fantasy Projection - We discussed this a bit in last week’s article, for tournament purposes it is not enough to simply evaluate players based on their expected fantasy value (mean, mean, mode, or whatever a single point-projection tends toward), but rather to think about players’ fantasy value as a probabilistic range of outcomes.
Player-to-Player Interaction - This concept is frequently referred to as “correlation”, and it is relevant to both players’ fantasy outcomes & their ownership. The core idea is that certain players’ outcomes & ownership levels are inherently linked to some degree or another.
One thing to note about all off the above is that it is impossible to know the true value of these variables prior to lock. For all of these, we have to make pre-lock assumptions that guide our way of thinking as we prepare tournament lineups.
To date, ASA has kept our eyes & quantitative attention on all of these components. We have projections, distributions, correlation, and ownership tools that help us evaluate all of these components individually. And of course the human brain can be quite effective at evaluating all of these components in unison. But the goal of a simulation system should be to incorporate all of these components into a quantitative & repeatable program that iterates and generates some sort of actionable output.
It is also worth noting, we there are so so many ways to skin this cat. Below I will outline the approach that we plan to take for the 2021-22 season, but note that it is not the only way to approach this problem, it is almost certainly not the best way to approach this problem. It will be an iterative approach for us, as we move through the 2021-22 season, so the current state might be quite different from the iteration we arrive at in January, or even September.
Ownership, Lineup Generation
If memory serves, this is the 5th NFL season of operation for ASA, to date we have never done ownership projections. But the goal is to provide ownership projections for the 2021 season. Rather than take a top-down approach to ownership - using historic data, current week projections, measuring industry buzz, etc - the plan is to project ownership through a bottom-up approach. If we take a set of baseline projections, a set that we feel mimics how the field will evaluate players & the slate, in theory we could generate some number of optimal lineups and store the exposure to every player of that optimal set. More or less, that’s what we intent to do.
But of course, tournament fields and the sets of lineups that make them up are governed by lineup construction mechanics that are (from a pure projection standpoint) sub-optimal. As such, as we attempt to build out hypothetical tournament fields, we need to try to inject some of these sub-optimal mechanics into lineup generation.
Stacking - Many lineups will stack players, the degree to which lineups will be stacked or correlated varies. Some proportion of lineups will feature a “double stack” vs. a “single stack” (QB + 2 pass-catchers vs. QB + 1 pass-catcher), some lineups will have a “bring back” (player rostered from team opposing core QB-receiver stack), some lineups will feature secondary “internal stacks” (e.g. skill players on opposing sides of a game that aren’t rostered with either’s QB), some lineups will prevent D/STs from being rostered against players opposing them, some lineups will insist on rostering a D/ST + running back pair. There is a latent probability that lineups take on these different structures. We have to make assumptions as to what those probabilities are to get good lineup creation iterations that are likely to mimic how the field builds lineups.
Projection Noise - Of course not every contestant in a tournament is using the same set of projections, so there is likely to be some noise around how the players selected to lineups. And of course many DFS players understand that optimizing towards projected fantasy points and pressing “Go” isn’t likely to be a winning strategy, so we do see ownership for players who project sub-optimally. As such, when generating possible lineups, we have to inject some artificial noise into the projections that govern lineup construction imitation.
Rather than try to generate X number of lineups for a tournament of X size, and iterating over that process by N number of desired simulations, our approach as of now is to generate a huge pool of possible lineups (roughly 50x the size of an arbitrary tournament) and sample lineups based on their probability of being selected. Our approach is to start with a quarterback, selecting a QB at random with probabilities of selection proportional the QBs’ values. Then we randomly sample lineup construction traits (e.g. stack size, whether to bring back an opponent, secondary stacking, RB + DST stacking, et al) based on assumed proportions of construction trait utilization among the field, and optimize lineups based on randomly selected lineup traits. We’re re-sampling lineup traits & QBs during each optimization iteration, re-injecting random projection noise during each iteration. In general, our view is that injecting randomness (whether through adding random projection noise or making random selections as to how a contestant might enter lineups) at as many steps as possible is a good thing. At the end of the day, people do wacky things, ownership tends to be pretty dispersed, and the combinations of players selected is impossibly hard to predict at a lineup-by-lineup level. At the end of the day, if we build 100k lineups and sample sets of 10k lineups (for a 10k-person tournament) a bunch of different times, we’re bound to get ownership & lineup build tendencies that are similar to what we expect to play out. Trying to predict the lineups that are eventually used in a 10k person tournament is an impossible task. Our goal is to try simulate the mechanics of 10k people building lineups under assumptions like projection, construction properties, et al and produce sets of lineups that mimic the distribution and properties of lineups that we expect to see.
Tournament Batches
As mentioned in the above section, once a large pool of hypothetical lineups are generated - with efforts to create a pool of lineups that mimic lineup construction properties & player selection distribution - we can simulate “random” lineup selection of batches of some arbitrary tournament size. I put “random” in quotation marks because it is not a purely random selection. Based on lineup features like raw projection (based on public projection set assumption) and lineup construction properties & the assumed rate at which they are deployed, we assign a score to each lineup that is proportional to the probability that it is selected. After selecting lineups to create our tournament lineup batches, we move on to simulating actual game outcomes.
Fantasy Outcomes
After we’ve simulated lineup batches, we now must simulate the fantasy outcomes of games/players by witch these batches of lineups will be ranked. In this section of the process, it will be important to consider properties like correlation & range of player outcomes.
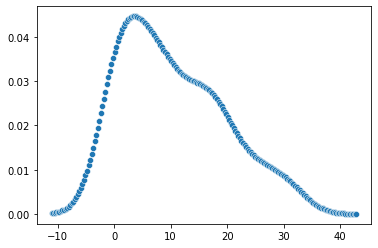
Let’s first start with players’ range of outcomes. While point-projection gives us an expected value for a player’s fantasy production (likely a mean or median outcome), that doesn’t really help us with simulation. If Derrick Henry projects for 30 fantasy points, of course we know more times than not he will score some value other than 30. A simple solution would be to assume all players’ range of outcomes is some normal distribution centered around their mean projection, with some either uniform standard distribution or some standard distribution proportional to their projection. But we know that this is simply not the case.
Players can have non-symmetrical distributions, or distributions with exceptionally wide or tight range of outcomes relative to their distribution center. As such, we need to not generate single “point-projections” for players, but rather a whole projection of outcomes and their relative probability. So rather than simulate over assumptions like “Stefon Diggs has a mean projection of 18 fantasy points”, simulate over assumptions like “Stefon Diggs range and probabilities of outcomes looks something like this”:
Ok, so we have not point projections for players, but projection distributions for players, we’re ready to simulate. For the purpose of our system, “simulate” means simply taking a random draw from players’ distributions, and assuming that for a specific simulation that is a players score, and then calculating what all the different players’ scores mean in the context of lineups selected for the specific simulation. Of course, it is not as simple as just making a bunch of random selections for the hundreds of active players, wash, rinse, repeat. Using the distribution above, if Stefon Diggs scores 30 fantasy points, it should give us a pretty solid indicator of the outcome of other players in the same game - Josh Allen, opposing QB or WRs, Emmanuel Sanders, etc. We must have a system for incorporating correlation.
While Allen’s range of outcomes mostly centers around fantasy totals in the mid-20s, we can see that if Diggs were to be assumed to score 30 fantasy points (give or take 5), Allen’s probability distribution should probably be shifted up a solid 5 to 7 fantasy points.
There is a difficult task of selecting the player to key correlated samples off of. The natural inclination might be to sample a QB outcome & then take correlated samples off of the QB sample. But opposing QBs are correlated, how do we decide with to make sample key? Take this year’s New Orleans Saints roster for example - might it be reasonable to assume that the performance of Alvin Kamara is more likely to influence peripheral outcomes than the performance of Jameis Winston? For individual simulations we go game by game, randomly select the “key player” (from whom we will anchor other players’ distribution samples) with probability of selection proportional to players’ mean projection, and then randomly select an outcome percentile (“key percentile”) for that player. Note that the probability of players achieving a certain percentile is equal across all distribution shapes - a player hitting their 50th percentile has a 1% probability, 51st percentile 1% probability, 99th percentile 1% probability. Based on the key player’s position, we assign correlative coefficients to peripheral players based on the key player’s position & each peripheral player’s position (I would love for use to adopt customized correlation coefficients based on player traits - the QB/RB correlation is likely to be significantly different between pairs like Herbert/Ekeler & Newton/Harris). Then, we pull samples from peripheral player distributions where probabilities of percentiles are not uniform, but skewed based on key percentile and coefficient. For example, if Diggs were randomly selected as the key player for Buffalo vs. Pittsburgh, and if a 90th percentile outcome were randomly selected for Diggs, the probability of percentiles nears 90th would increase for Allen samples, probability of percentiles for negatively correlated players like the Pittsburgh DST would decrease on the opposite side of the 50th percentile. I don’t want to go into too many details on the function used to re-generate players’ distributions conditional on key player samples as it is currently a complex function and one that we are still experiment with.
But in short, by iterating over individual games, taking player samples that are a mix of random and correlated, we can begin to build out a set of simulations for player outcomes that we can then match to the lineup generation/tournament batches, and then score tournament lineups based on realized return.
Lineup Scoring
So now we have batches of lineups (which combine to make tournament field batches), and we have batches of player outcomes (which are thoughtfully correlated as we might expect games to unfold). Figuring out how to score players through these simulations isn’t perfectly intuitive. We could just have an app that prints out the 1000 winning lineups from 1000 simulations, but I’m not sure that’s super actionable. We could store (and list in our projections) players’ propensity to appear in the top 1% of lineups from 1000 simulations. But if Joe Mixon is 50% owned an appears in 20% of Top-1% lineups but the remaining 49.8% of Mixon lineups all brick out (in the simulations), we’re not so sure that that would mean he’s a better play than e.g. a 5% owned Ronald Jones who appears in 15% of Top-1% lineups. And of course “Top 1%” can be a bit of an arbitrary number, just focusing on propensity to be in winning lineup can be a bit noisy. Instead, our current approach is to store the relative (to entry fee) return of e.g. all lineups that feature Joe Mixon and store this as a sort of “simulation value”. That is, if Mixon is featured in 50% of lineups & half of them brick, half of them 2x you’re looking at an average value of: 0.5 * 0x + 0.5 * 2x = 1x, or essentially +0% average value. If 70% of Mixon lineups brick, 20% 2x, 9% 3x, and 1% 100x, you’re looking at a value of: (0.7 * 0x + 0.2 * 2x + 0.09 * 3x + 0.01 * 100x) = 1.67x, or +67% average return. In the second scenario, even though the vast majority of Mixon lineups result in a whiff, the average return on Mixon lineups is still +EV.
We’ll continue to refine our approach on simulation player scoring. One alternative could be to store players propensity to be rostered inside the Top 1% minus their ownership (one might call this “leverage”), but this can be a difficult metric to optimize towards as rostering all the highest-leverage plays together (using an optimization program) might give you a bunch of lineups that are high leverage, but fall well below the salary cap and thus have a low chance of winning.
As mentioned at the top, this is far from the end-all-be-all of simulation. It is a raw approach that we will continue to refine. If you have any questions or ideas for possible improvements, perhaps your own approach to lineup & fantasy simulation please feel free to share with us via Twitter or email.